‌

Modeling

Having done all that we can put it together to create a molecule like propylene-oxide

With[{XOCAngle=30°,
  OCDist=1.5/(2*Sin[30°]),
  CCDist=1.5,
  CCCAngle=-120°,
  CCCODihed=60°,
  CHDist=1.2,
  CHAngle=120°,
  CHDihed=120°},
 Molecule@{
  {"O"},
  {"X",1,1},
  {"C",1,OCDist,2,XOCAngle},
  {"C",1,OCDist,2,-XOCAngle},
  {"C",4,CCDist,3,CCCAngle,1,CCCODihed},
  {"H",5,CHDist,4,CHAngle},
  {"H",5,CHDist,4,CHAngle,6,CHDihed},
  {"H",5,CHDist,4,CHAngle,7,CHDihed},
  {"H",4,CHDist,3,CCCAngle,1,-CCCODihed},
  {"H",3,CHDist,4,CCCAngle,1,CCCODihed},
  {"H",3,CHDist,4,CCCAngle,1,-CCCODihed},
  {1,4,1},
  {1,3,1},
  {3,4,1},
  {4,5,1},
  {6,5,1},
  {7,5,1},
  {8,5,1},
  {9,4,1},
  {10,3,1},
  {11,3,1}
  }]//DisplayMolecule

(*Out:*)

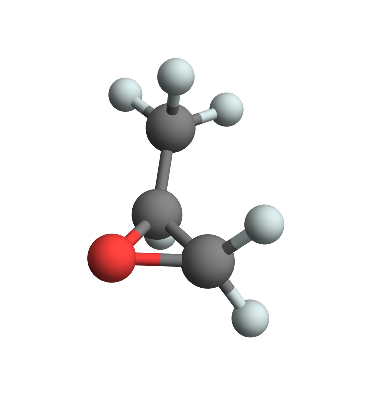
But we are, of course, not merely restricted to drawing molecules. We could easily extend this to getting, say, the center of mass or moments of inertia of our molecule.

CenterOfMass[m_Molecule]:=;
MomentsOfInertia[m_Molecule]:=;

We can do even more interesting things, though.

Say we had some guess for what the electric field looked like around a given type of atom, maybe as an association of functions:

EFTable=Association@Table[
 ElementData[element,"Symbol"]Function[{atom,testChargePosition},
  With[{d=Norm@(atom["Position"]-testChargePositions)},
   Replace[d-UnitConvert[atom["Radius"],"Angstroms"],{
     v_?NonPositive((1+v)/d)2,
     v_(1/d2)
     }]
   ]
  ],
 {element,ElementData[]}]

Then say we can approximate how this distributes across different degrees of bond conjugation:

EFBondFactor=<||>;

We could then provide a rough guess for the electric field of the molecule:

EFGuess[m_Molecule]:=;

And then we could plot it with ContourPlot