‌

Dynamic

Everything done up to here has involved static content. Often, though, dynamic content is what you need. I don’t have the time to explain all of Dynamic here, given how many things one can do with Dynamic , but it’s worth going over a few critical things.

Dynamic as formatting head

Dynamic only ever updates while it’s on screen. This is one of it’s key features, as otherwise things could get out of hand. How this works is that Dynamic is just something that the Mathematica front end sees and creates listeners to update.

This means, though, that if your content will never display it won’t update. If you need an invisible updater, use DynamicWrapper .

Dynamic’s second argument

Dynamic takes a function as a second argument that it calls whenever it tries to update, passing the update value as the first argument. We can use this to do fancy things like the following:

Slider@Dynamic[x, (x = RandomReal[]) &]

(*Out:*)

The variable takes a random value every time we try to update it.

This could also be used to record responses:

$responseCache = {};
Grid[
  {
    {
      SetterBar[
        Dynamic[Last@Replace[$responseCache, {} :> {None}],
          AppendTo[$responseCache, #] &
          ],
        Range[10]
        ],
      Dynamic@Column@$responseCache
      }
    },
  Alignment -> Top
  ]

(*Out:*)

Each click adds to the response cache.

TrackedSymbols

Dynamic usually decides in a semi-opaque manner which symbols to track changes in, but we can force it to follow symbol updates. Let’s make a Dynamic thing that passes colors back and forth. We’ll write it using Mouseover so the passing only occurs when we’re hovering

c1 = Gray; c2 = Green; counter = 1;
Mouseover[
  Row@{Dynamic@Graphics[{c1, Disk[]}], Dynamic@Graphics[{c2, Disk[]}]},
  Row@{
     Dynamic[Graphics[{
          c1 = If[counter < 5,
             counter++; Pause[.1]; c1,
             counter = 1; c2],
          Disk[]}],
      TrackedSymbols :> {c1, c2, counter}],
    Dynamic[Graphics[{
         c2 = If[c1 === c2, RandomColor[], c2],
         Disk[]}], TrackedSymbols :> {c1, c2, counter}]
    }
 ]

(*Out:*)

You’ll notice this works exactly as expected.

Often, however, one runs into issues with TrackedSymbols . This is because of an interesting implementation choice. To track a symbol, it needs to appear in the display expression and not too deep. Usually I simply put the symbol in as part of a CompoundExpression so it does nothing, but Dynamic knows to track it. The following is probably the safer way to write this, to ensure tracking:

c1 = Gray; c2 = Green; counter = 1;
Mouseover[
  Row@{Dynamic@Graphics[{c1, Disk[]}], Dynamic@Graphics[{c2, Disk[]}]},
  Row@{
     Dynamic[counter; c1; c2; Graphics[{
          c1 = If[counter < 5,
             counter++; Pause[.1]; c1,
             counter = 1; c2],
          Disk[]}],
      TrackedSymbols :> {c1, c2, counter}],
    Dynamic[c1; c2; Graphics[{
         c2 = If[c1 === c2, RandomColor[], c2],
         Disk[]}], TrackedSymbols :> {c1, c2, counter}]
    }
 ]

(*Out:*)

UpdateInterval

Dynamic can also be scheduled to simply update on a given time frame, which is usually a fall back for when there’s no other way to get symbol tracking to work right or there are no symbols to track. In this case it’s very important the TrackedSymbols be passed an empty list.

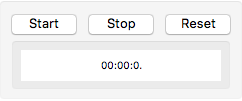
Here’s a classic stop watch example:

startTime = None; updateInterval = ∞;
Panel@Grid[{
     {Button["Start",
         startTime = TimeObject[];
         updateInterval = .1],
       Button["Stop", updateInterval = ∞],
       Button["Reset", 
     startTime = 
      If[updateInterval === ∞, None, TimeObject[]]]
       },
     {Panel@Panel[
          Dynamic[
            updateInterval;
            startTime;
            Dynamic[
              TemplateApply["``:``:``",
                If[MatchQ[#, _Integer],
                    StringPadLeft[ToString[#], 2, "0"],
                    ToString@#] & /@ First@TimeObject@(
                     If[
                       startTime === None,
                       {0, 0, 0},
                       {0, 0, 
               Round[TimeObject[] - startTime // 
                 QuantityMagnitude, .01]}])
                ],
              TrackedSymbols :> {},
              UpdateInterval -> updateInterval],
            TrackedSymbols :> {updateInterval, startTime}],
          ImageSize -> 200,
          Alignment -> Center,
          Background -> White],
       SpanFromLeft}
     }]

(*Out:*)