‌

Calculus

Mathematica is useful for many types of mathematical operations, but of particular use are derivatives and integrals.

Derivatives

Derivatives can be taken using either the function D or the alias pd.

For example, to take the first derivative of x² one can use either of the following:

D[x^2, x]

(*Out:*)

2 x

or

∂xx^2

(*Out:*)

2 x

A derivative can be taken of a derivative:

∂x∂xx^2

(*Out:*)

2

But this is equivalent to a simple second derivative which Mathematica can also do:

D[x^2, {x, 2}]

(*Out:*)

2

or

∂x,xx^2

(*Out:*)

2

We can also take derivatives in multiple variables:

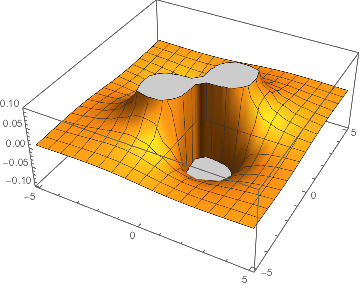
∂x,y

(3 x y)/(x^2+y^2)^(5/2)

And then for fun let’s plot this:

dxy = \!\(
\*SubscriptBox[\(∂\), \(x, y\)]
\*FractionBox[\(1\), 
SqrtBox[\(
\*SuperscriptBox[\(x\), \(2\)] + 
\*SuperscriptBox[\(y\), \(2\)]\)]]\);
Plot3D[dxy, {x, -5, 5}, {y, -5, 5}]

(*Out:*)

Integration

Mathematica also knows how to do more integrals than any chemist is likely to need. The function for integration is Integrate although like with derivatives there is an alias via intt for indefinite integrals and dintt for definite integrals

Examples:

Integrate[2, x]

(*Out:*)

2 x

∫2 x

(*Out:*)

2 x

And just to show that Mathematica observes the fundamental theorem of calculus like the rest of us:

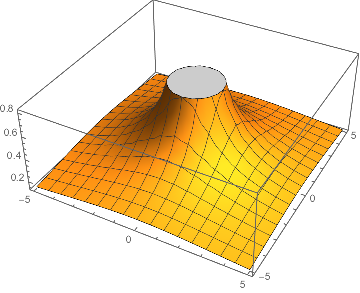
∫∫dxy x y

1/Sqrt[x^2+y^2]

And we’ll plot this guy too:

reversedxy = ∫∫dxy x
y;
Plot3D[reversedxy, {x, -5, 5}, {y, -5, 5}]

(*Out:*)

Fun examples:

Mathematica is a great calculus tool and it knows many types of interesting functions so we’ll have it integrate the following very nasty function for us:

Subscript[P, 3](cos(θ)) cot(θ) d/dθ Subscript[P, 4](cos(θ)) where Subscript[P, i](cos(θ)) is the ith Legendre polynomial in cos(θ), which is to say, a nasty polynomial with a lot of trigonometric functions which is very difficult to integrate.

Integrate[
 LegendreP[3, Cos[θ]] Cot[θ] D[
   LegendreP[4, Cos[θ]], θ], {θ, 0, π}]

(*Out:*)

0

but Mathematica has absolutely no problem evaluating this integral. It can even tell you that switching the derivative and cot terms makes the integral impossible to evaluate.

Integrate[
 LegendreP[3, Cos[θ]] D[
   Cot[θ] LegendreP[4, Cos[θ]], θ], {θ, 
  0, π}]

∫0π (-3 Cos[θ]+5 Cos[θ]3) (- (3-30 Cos[θ]2+35 Cos[θ]4) Csc[θ]2+ Cot[θ] (60 Cos[θ] Sin[θ]-140 Cos[θ]3 Sin[θ]))θ

And when it sees that it simply returns the integration expression.